来源：力扣（LeetCode）

描述：

n 座城市和一些连接这些城市的道路 roads 共同组成一个基础设施网络。每个 roads[i] = [ai, bi] 都表示在城市 ai 和 bi 之间有一条双向道路。

两座不同城市构成的 城市对 的 网络秩 定义为：与这两座城市 直接 相连的道路总数。如果存在一条道路直接连接这两座城市，则这条道路只计算 一次 。

整个基础设施网络的 最大网络秩 是所有不同城市对中的 最大网络秩 。

给你整数 n 和数组 roads，返回整个基础设施网络的 最大网络秩 。

示例 1：

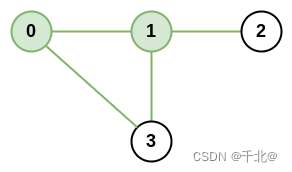
输入：n = 4, roads = [[0,1],[0,3],[1,2],[1,3]]
输出：4
解释：城市 0 和 1 的网络秩是 4，因为共有 4 条道路与城市 0 或 1 相连。位于 0 和 1 之间的道路只计算一次。

示例 2：

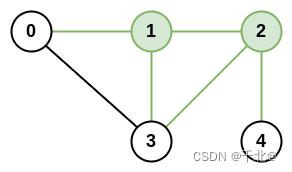
输入：n = 5, roads = [[0,1],[0,3],[1,2],[1,3],[2,3],[2,4]]
输出：5
解释：共有 5 条道路与城市 1 或 2 相连。

示例 3：

输入：n = 8, roads = [[0,1],[1,2],[2,3],[2,4],[5,6],[5,7]]
输出：5
解释：2 和 5 的网络秩为 5，注意并非所有的城市都需要连接起来。

提示：

• 2 <= n <= 100
• 0 <= roads.length <= n * (n - 1) / 2
• roads[i].length == 2
• 0 <= ai, bi <= n-1
• ai != bi
• 每对城市之间 最多只有一条 道路相连

方法一：枚举

思路与算法

根据题意可知，两座不同城市构成的城市对的网络秩定义为：与这两座城市直接相连的道路总数，这两座城市之间的道路只计算一次。假设城市 x 的度数为 degree[x]，则此时我们可以知道城市对 (i, j) 的网络秩为如下：

• 如果 i 与 j 之间没有道路连接，则此时 (i, j) 的网络秩为 degree[i] + degree[j]；
• 如果 i 与 j 之间存在道路连接，则此时 (i, j) 的网络秩为 degree[i] + degree[j] − 1；

根据以上求网络秩的方法，我们首先求出所有城市在图中的度数，然后枚举所有可能的城市对 (i, j)，求出城市对 (i, j) 的网络秩，即可找到最大的网络秩。

代码：

class Solution {
public:int maximalNetworkRank(int n, vector>& roads) {vector> connect(n, vector(n, false));vector degree(n, 0);for (auto v : roads) {connect[v[0]][v[1]] = true;connect[v[1]][v[0]] = true;degree[v[0]]++;degree[v[1]]++;}int maxRank = 0;for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {int rank = degree[i] + degree[j] - (connect[i][j] ? 1 : 0);maxRank = max(maxRank, rank);}}return maxRank;}
};

执行用时：60 ms, 在所有 C++ 提交中击败了66.76%的用户
内存消耗：30.6 MB, 在所有 C++ 提交中击败了38.27%的用户
复杂度分析
时间复杂度：O(n²)，其中 n 表示给城市的数目。我们需要枚举所有可能的城市对，最多有 n²个城市对。
空间复杂度：O(n²)。需要记录图中所有的城市之间的连通关系，需要的空间为 O(n²)。如果用邻接表存储连通关系，空间复杂度可以优化到 O(n+m)，其中 m 表示 roads 的长度。

方法二：贪心

思路与算法

我们可以对解法一中的方法继续优化。设 first 表示所有节点中度数的最大值，second 表示所有节点中度数的次大值，实际我们只需要考虑度数为最大值与次大值的城市即可，其余即可城市可以无须考虑，原因如下：

• 已知最大值 first 与次大值 second，则此时可以知道当前最差的情况下，假设这两城市存在连接，则最大的网络秩为 first + second − 1；
• 假设存在度数比 second 的城市 x，则此时 degree[x] < second，此时含有 x 构成的城市对的最大网络秩不超过 degree[x] + first，此时一定满足 degree[x] + first ≤ second + first；

综上可以得出结论选择最大或者次大度数的城市一定是最优的。我们可以求出度数为 first 的城市集合 firstArr，同时求出度数为 second 的城市集合 secondArr。设城市的总数量为 n，道路的总数量为 m，集合 firstArr 的数量为 x，则此时该集合可以构造的城市对数量为 x(x−1)2\frac{x(x-1)}{2}2x(x−1)​ ，分以下几种情况来讨论:

• 如果 x = 1，此时我们必须选择 firstArr 中唯一的城市，另一个城市只能在 secondArr 中选择，枚举 secondArr 中的每个城市，找到最大的网络秩即可，此时需要的时间复杂度为 O(n)；
• 如果 x>1 时，分类讨论如下：
  • 如果满足 x2\frac{x}{2}2x​ > m 时，此时集合 firstArr 一定存在一对城市，他们之间没有道路连接，此时最大的网络秩即为 2 × first；
  • 如果满足 x2\frac{x}{2}2x​ ≤ m 时，此时枚举集合 firstArr 中所有不同的城市对即可，此时不需要再考虑次大的城市集合 secondArr，因为此时一定满足 2 × first − 1 ≥ first + second > 2 × second ，此时时间复杂度不超过 O(m)；

因此通过以上分析，上述解法的时间复杂度为 O(n+m)。

代码：

class Solution {
public:int maximalNetworkRank(int n, vector>& roads) {vector> connect(n, vector(n, false));vector degree(n);for (auto road : roads) {int x = road[0], y = road[1];connect[x][y] = true;connect[y][x] = true;degree[x]++;degree[y]++;}int first = -1, second = -2;vector firstArr, secondArr;for (int i = 0; i < n; ++i) {if (degree[i] > first) {second = first;secondArr = firstArr;first = degree[i];firstArr.clear();firstArr.emplace_back(i);} else if (degree[i] == first) {firstArr.emplace_back(i);} else if (degree[i] > second){secondArr.clear();second = degree[i];secondArr.emplace_back(i);} else if (degree[i] == second) {secondArr.emplace_back(i);}}if (firstArr.size() == 1) {int u = firstArr[0];for (int v : secondArr) {if (!connect[u][v]) {return first + second;}}return first + second - 1;} else {int m = roads.size();if (firstArr.size() * (firstArr.size() - 1) / 2 > m) {return first * 2;}for (int u: firstArr) {for (int v: firstArr) {if (u != v && !connect[u][v]) {return first * 2;}}}return first * 2 - 1;}}
};

执行用时：60 ms, 在所有 C++ 提交中击败了66.76%的用户
内存消耗：30.7 MB, 在所有 C++ 提交中击败了36.59%的用户
复杂度分析
时间复杂度：O(n+m)，其中 n 表示给定的数字 n，m 表示城市之间的道路总数。计算城市的度数需要的时间为 O(m)，找到城市中最大度数和次大度数城市集合需要的时间为 O(n)，计算城市对中最大的网络秩需要的时间为 O(m)，因此总的时间复杂度为 O(m+n)。
空间复杂度：O(n²)。需要记录图中所有的城市之间的联通关系，需要的空间为 O(n²)，记录所有节点的度需要的空间为 O(n)，记录最大度数与次大度数的城市集合需要的空间为 O(n)，因此总的空间复杂度为 O(n²)。如果用邻接表存储连通关系，空间复杂度可以优化到 O(n+m)，其中 m 表示 roads 的长度。
author：LeetCode-Solution