下面是我基于opencascade英文文档中关于occt_modeling_data中Properties of Shapes部分进行的翻译，英文好的还是建议直接看文档，部分我不肯定的地方我会附上英文原句。如发现有错误欢迎评论区留言。

文章目录

• 形状的局部属性(Local Properties of Shapes)
• Local Properties of Curves and Surfaces
• 曲线和曲面的连续性(Continuity of Curves and Surfaces)
• 共享边的正则度(Regularity of Shared Edges)
• 形状的全局属性(Global Properties of Shapes)
• 曲线和曲面适应器(Adaptors for Curves and Surfaces)

形状的局部属性(Local Properties of Shapes)

BRepLProp 包提供了 Local Properties of Shapes 组件，这个组件包含了计算一个 BRep 模型中边和面的多种局部属性的算法。

可以被查询的局部属性有：

• 对于边对应曲线上参数为u的一点
  1. 点(point)
  2. 导数向量(derivative vector)，至多三阶导(degree)
  3. 切向量(tangent vector)
  4. 法向量(normal)
  5. 曲率(curvature)，以及曲率中心(center of curvature)
• 对于面对应曲面上参数为(u,v)的一点
  1. 点(point)
  2. 导数向量(derivative vector)，至多二阶导(degree)
  3. 对于u和v同参数曲线的切向量(tangent vectors)
  4. 法向量(normal vector)
  5. 最小或最大曲率(the minimum or maximum curvature)，以及对应的曲率方向
• 对于边对应曲线的连续性阶数(the degree of continuity)，这里的连续性是在，由两个不同的边连接(concatenation)构建而形成的连接点(junction point)处的连续性。

解析曲线和曲面被描述为 BRepAdaptor 曲线和曲面，给形状提供了描述它们几何支持(geometric support)的接口。对于局部的属性的基点是由曲线上参数 u 定义，或由曲面上 (u,v) 参数定义。

Local Properties of Curves and Surfaces

”Local Properties of Curves and Surfaces" 组件提供了计算在一个 Geom 曲线或曲面上(in 2D or 3D space)计算不同局部属性的算法。主要包括：

• Geom2dLProp 包，允许对于一条2D曲线上的一点，计算导数向量和切向量(法向量和曲率)
• GeomLProp 包，提供了对于3D曲线或曲面上，局部属性的计算
• LProp包，提供了用于特征化2D曲线上一个特定点的枚举类型

曲线要么是 Geom_Curve 曲线(3D空间内)或 Geom2d_Curve 曲线(平面内)。曲面是 Geom_Surface 曲面。需要计算局部属性的点由它在曲线上的参数 u 定义或由它在曲面上的参数 (u,v) 定义。

那是可能地去查询上述提及的对于具有相同局部属性的点的，以及额外对于2D曲线中具有上述局部属性的点的查询

• 对应于曲率的最小或最大值的点
• 拐点(inflection points)

Example: How to check the surface concavity

为了检查一个曲面的凹凸性(concavity)，过程如下：

1. 采样曲面，然后计算在每个点处的高斯曲率(Gaussian curvature)
2. 如果曲率的值的符号变化了，曲面依据所看的点定义凹形或凸性
3. 为了计算一个高斯曲率(Gaussian curvature)，使用 GeomLProp 中的 SLprops 类，这是从 LProp 中的通用类 SLProps 实例化来的，然后使用方法 GaussianCurvature。

曲线和曲面的连续性(Continuity of Curves and Surfaces)

在 GeomAbs_Shape 枚举类型描述了曲线和曲面支持的连续性的类型。

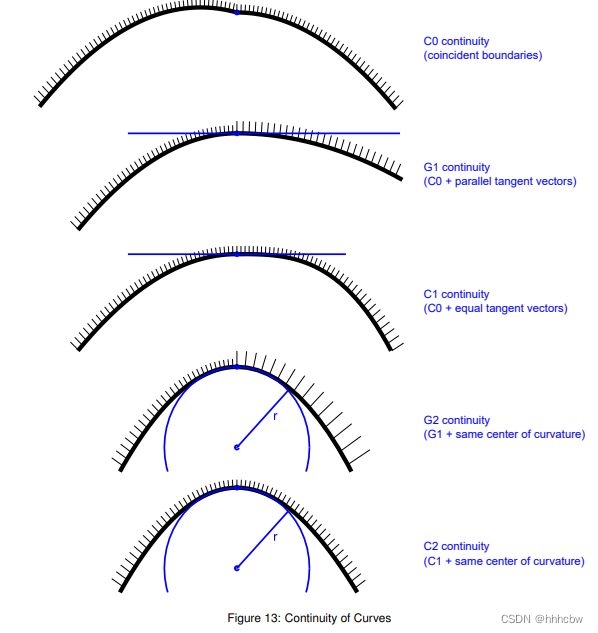
对于曲线，如下连续性的类型是可支持的(如下图)：

• C0 (GeomAbs_C0) —— 参数连续性。它与G0(几何连续性)是一致的，所以G0没有单独变量表示。
• G1(GeomAbs_G1) —— 左曲线的切向量和右曲线的切向量是平行的。
• C1(GeomAbs_C1) —— 暗示一阶导的连续性
• G2(GeomAbs_G2) —— 在G1连续的基础上，左曲线和右曲线的曲率中心是相同的
• C2(GeomAbs_C2) —— 一直到二阶导都是连续的
• C3(GeomAbs_C3) —— 一直到三阶导都是连续的
• CN(GeomAbs_CN) —— 一直到N阶到都是连续的(连续的无穷阶)

注意：几何连续性(G1,G2)意味着曲线可以被重参数化为有(C1,C2)连续性。

下述曲面连续性的类型是支持的：

• C0(GeomAbs_C0) —— 参数连续性(曲面没有不连续的点或曲线)
• G1(GeomAbs_G1) —— 曲面在每个点只有一个切平面
• C1(GeomAbs_C1) —— 暗示一阶导的连续性
• G2(GeomAbs_G2) —— 在G1连续性的基础上，主曲率和方向是连续的
• C2(GeomAbs_C2) —— 直到二阶导都是连续的
• C3(GeomAbs_C3) —— 直到三阶导都是连续的
• CN(GeomAbs_CN) —— 直到N阶导都是连续的(连续的无穷阶)

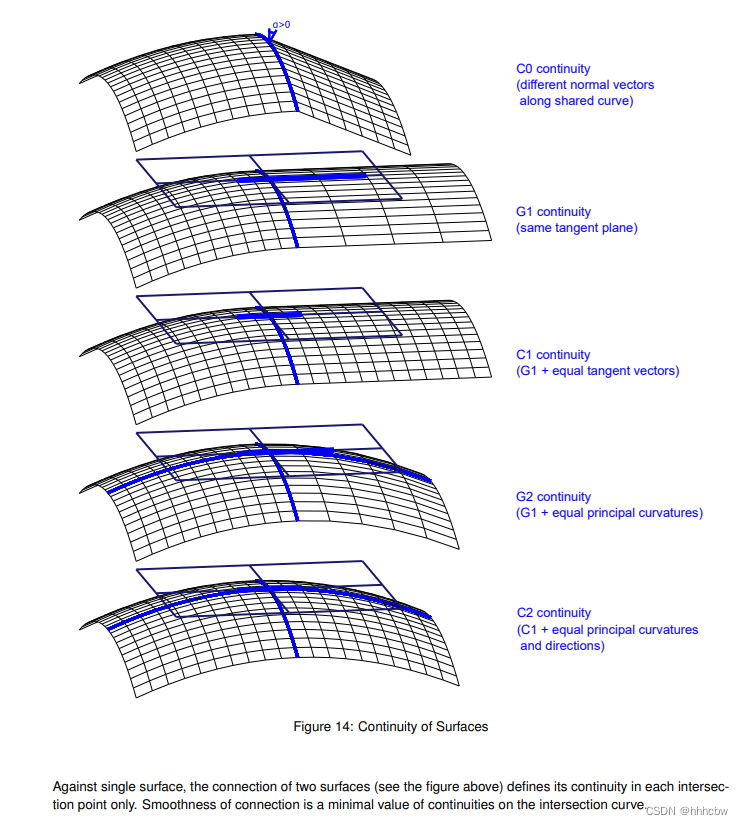
与单一曲面不同，两个曲面的连接(看上图)只在每个交点处定义连续性。连接的光滑程度是交线连续性的一个最小值。

共享边的正则度(Regularity of Shared Edges)

一条边的正则度是两个共享这条边的面连接的光滑度。换句话说，正则度是两个面连接边的每个点的中的最小的连续性。

边的正则度可以有 BRep_Builder::Continuity 方法设置。使用 BRep_Tool::Continuity 方法得到正则度。

一些算法，比如 Fillet 设置有它们自己算法创造边的正则度。也就是说，其他算法(比如Boolean Operations，Shape Healing等)不会设置正则度。如果正则度需要在一个形状上正确设置，可以使用 BRepLib::EncodeRegularity。它对形状的每个边都计算和设置了正确的值。

正则度标记可以通过如下高等算法扩展使用：Chamfer, Draft Angle, Hidden Line, Removal, Gluer。

形状的全局属性(Global Properties of Shapes)

The Global Properties of Shapes 组件提供了计算3D空间中一个复合几何系统的全局属性，以及查询计算结构的框架。

对于一个系统全局属性有：

• 质量(mass)
• 质心(mass center)
• 惯性张量(matrix of inertia)
• 关于一个轴的矩(moment about an axis)
• 关于一个轴的惯性半径(radius of gyration about an axis)
• 惯性的主属性，比如主轴(principal axis)，主矩(principal moments)和主惯性半径(principal radius of gyration)

几何系统是以形状通用定义的。根据它们被解析的方式，这些形状将给出如下几何系统的属性：

• 由边的形状产生的线(lines)
• 由面的形状产生的曲面(surfaces)
• 由形状围成的刚体产生的体(volumes)

几个系统的全局属性可能会被组合，来给出有这些系统组合而成的系统的全局属性。

Global Properties of Shapes 组件由如下组成：

• 七个函数去计算一个形状的全局属性：对于线一个函数，对于曲面两个函数，对于体四个函数。函数的选择依赖输入的参数和计算使用的算法(BRepGProp global functions)。
• 对于点集计算全局属性的一个框架(GProp_PGProps)
• 一个通用框架去组合由集合更基础框架保存的全局属性，然后提供一个通用编程接口去查阅计算完的全局属性。

GeomLProp 和 Geom2dLProp 包提供了计算曲线和曲面局部属性的算法。

一个曲线(有一个参数)有如下局部属性：

• 点(Point)
• 导数(Derivative)
• 切线(Tangent)
• 法线(Normal)
• 曲率(Curvature)
• 曲率中心(Center of curvature)

一个曲面(有两个参数U和V)有如下局部属性：

• 点(Point)
• 关于U和V的偏导(derivative for U 和 V)
• 切线(tangent line for U and V)
• 法线(normal)
• 最大曲率(max curvature)
• 最小曲率(min curvature)
• 曲率的主方向(main directions of curvature)
• 平均曲率(mean curvature)
• 高斯曲率(Gaussian curvature)

如下方法是可用的：

• CLProps —— 计算一条曲线的局部属性(tangency, curvature, normal)
• CurAndInf2d —— 计算2d曲线的最大和最小曲率以及极值点(inflection points)
• SLProps —— 计算一个曲面的局部属性(tangency, the normal and curvature)
• Continuity —— 计算两条曲线交点处的正则度。

注意 B-spline 曲线和曲面被接受，但不会被切为期望连续性的片段。正如所见，这是全局连续性。

曲线和曲面适应器(Adaptors for Curves and Surfaces)

一些 Open CASCADE Technology 通用算法理论上是对所有类型的曲线和曲面都奏效。

为了这个目的，它们简单地通过一个得到需要解析曲线或曲面的服务，就是一个单一的API，不管曲线和曲面的类型。这些接口被称为适应器(adaptors)

例如，Adaptor3d_Curve 是提供通过使用任意3D曲线的算法这样服务的抽象类。

GeomAdaptor 包提供了接口：

• 在一个Geom曲线
• 在位于一个Geom曲面中的曲线
• 在一个Geom曲面

Geom2dAdaptor 包提供了接口：

• 在一个 Geom2d 曲线

BRepAdaptor 包提供了接口：

• 在一个面
• 在一条边

当你写了一个操作几何物体的算法，使用 Adaptor3d（或 Adaptor2d）物体。

因此，你可以对于任意类别的物体使用算法，只要你提供给这个物体一个源于 Adaptor3d 或 Adaptor2d 的接口。这些接口是易于使用的：只需简单地从一个 Geom2d 曲线创建一个适应曲线或曲面，然后使用使用这个适应曲线作为算法的参数。