一、重新安排行程

题目描述：

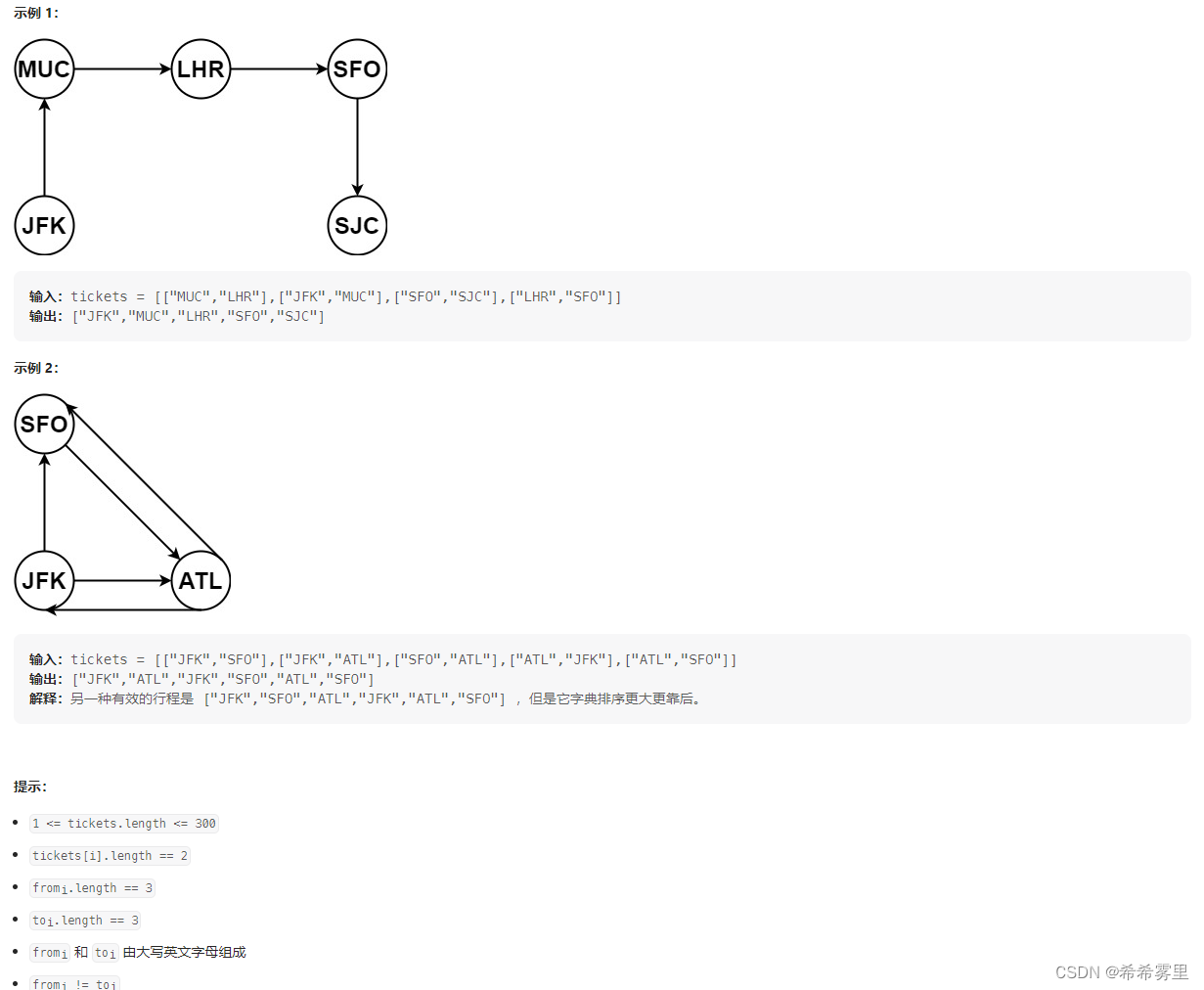
给你一份航线列表 tickets ，其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。

所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。

• 例如，行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小，排序更靠前。

假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。

 思路和想法：

        这道题目用回溯法解决，这道题目有几个难点如下：

• 一个行程中，如果航班处理不好容易变成一个圈，成为死循环
• 有多种解法，字母序靠前排在前面，如何记录映射关系？
• 使用回溯法的话，终止条件是什么呢？
• 搜索的过程中，如何遍历一个机场所对应的所有机场。

class Solution {
private:
// unordered_map<出发机场, map<到达机场, 航班次数>> targets
unordered_map> targets;
bool backtracking(int ticketNum, vector& result) {if (result.size() == ticketNum + 1) {return true;}for (pair& target : targets[result[result.size() - 1]]) {if (target.second > 0 ) { // 记录到达机场是否飞过了result.push_back(target.first);target.second--;if (backtracking(ticketNum, result)) return true;result.pop_back();target.second++;}}return false;
}
public:vector findItinerary(vector>& tickets) {targets.clear();vector result;for (const vector& vec : tickets) {targets[vec[0]][vec[1]]++; // 记录映射关系}result.push_back("JFK"); // 起始机场backtracking(tickets.size(), result);return result;}
};

二、N皇后

题目描述：

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

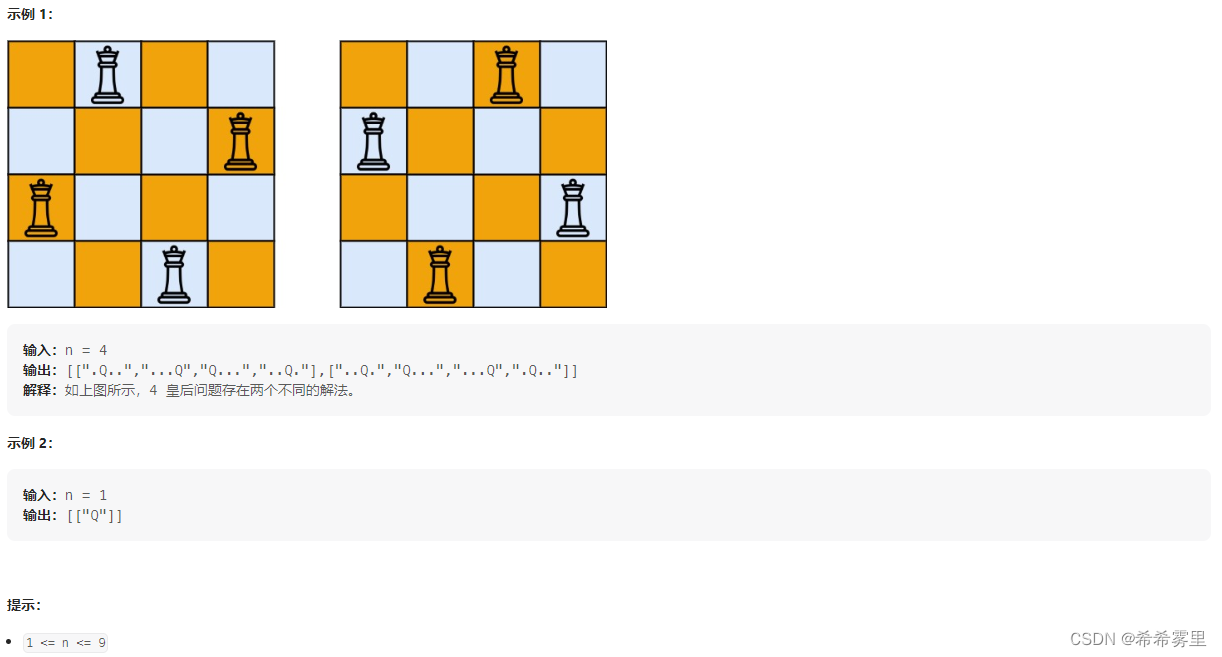
给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

思路和想法：

（1）根据题意，皇后们的约束条件：

• 不能同行
• 不能同列
• 不能同斜线

  这里的斜线，需要注意的是有45度角和135度角两种情况，并且是在当前以上的所有行斜线上有无‘Q’，有则不执行，继续递归。

（2）回溯三部曲中的单层逻辑

满足以上的约束条件，则当前chessboard[row][col] = 'Q';

class Solution {
public:
vector> result;
//cow为列，row为行
bool isVaild(int row,int col, vector& chessboard, int n){for(int i = 0; i < row; i++){//检查列if (chessboard[i][col] == 'Q'){return false;}}//检查45度角是否有皇后for (int i = row - 1, j = col - 1; i >=0 && j >= 0 ; i--, j--){if (chessboard[i][j] == 'Q'){return false;}}//检查135度角是否有皇后for (int i = row - 1, j = col + 1; i >=0 && j < n ; i--, j++){if (chessboard[i][j] == 'Q'){return false;}}return true;
}void backtracing(int n,int row, vector& chessboard){//终止条件if(row == n){result.push_back(chessboard);return;}//单层搜索逻辑for(int col = 0; col < n;col++){if(isVaild(row, col, chessboard, n)){chessboard[row][col] = 'Q';backtracing(n, row + 1,chessboard);chessboard[row][col] = '.';}}
}
vector> solveNQueens(int n) {result.clear();std::vector chessboard(n, std::string(n, '.'));backtracing(n, 0, chessboard);return result;
}
};

 三、解数独

题目描述：

编写一个程序，通过填充空格来解决数独问题。

数独的解法需 遵循如下规则：

1. 数字 1-9 在每一行只能出现一次。
2. 数字 1-9 在每一列只能出现一次。
3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

数独部分空格内已填入了数字，空白格用 '.' 表示。

思路和想法： 

（1）根据题意，这里的约束条件

• 数字1-9在一行只能出现1次
• 数字1-9在一列只能出现1次
• 数字1-9在3*3宫内只能出现1次

（2）推导逻辑

遍历行和列，当前遍历位置元素为空时，尝试将1到9都尝试一遍，判断是否满足约束条件，满足则继续，不满足则回溯。

class Solution {
private:
bool backtracking(vector>& board) {for (int i = 0; i < 9; i++) {                       //行for (int j = 0; j < 9; j++) {                   //列if (board[i][j] == '.') {for (char k = '1'; k <= '9'; k++) {     if (isValid(i, j, k, board)) {board[i][j] = k;                // 放置kif (backtracking(board)) return true; // 如果找到合适一组立刻返回board[i][j] = '.';              // 回溯，撤销k}}return false;  }}}return true; // 遍历完没有返回false，说明找到了合适棋盘位置了
}
bool isValid(int row, int col, char val, vector>& board) {for (int i = 0; i < 9; i++) {       //行重复if (board[row][i] == val) {return false;}}for (int j = 0; j < 9; j++) {       // 列重复if (board[j][col] == val) {return false;}}int startRow = (row / 3) * 3;int startCol = (col / 3) * 3;for (int i = startRow; i < startRow + 3; i++) { // 9方格重复for (int j = startCol; j < startCol + 3; j++) {if (board[i][j] == val ) {return false;}}}return true;
}
public:void solveSudoku(vector>& board) {backtracking(board);}
};