LeetCode 环形链表 II 的通俗易懂理解
代码可以参考
https://leetcode.cn/problems/linked-list-cycle-ii/solution/142-huan-xing-lian-biao-ii-jian-hua-gong-shi-jia-2/
网上找了很多答案,感觉他们理解还是差了一点
本文讲的是快慢指针那种解法
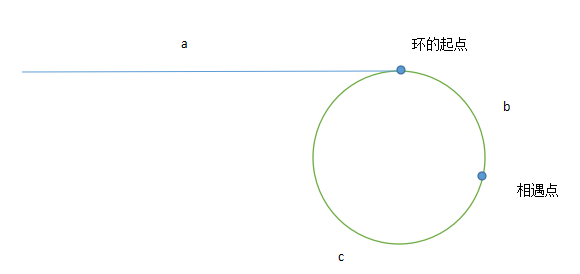
首先
a 为到达环起点距离
b为环的起点-》相遇点的距离
c为相遇点-》环的起点的距离
快指针的速度为慢指针的两倍
a+b为慢指针走过的距离,b+c为环的大小,快指针可能领先慢指针n圈,所以下面公式为n倍的 b+c等号左边为慢指针走过的距离,右边为快指针走过的距离
(a + b) * 2 = a + b + n (b + c)
推导
a + b + a + b = a + b + n (b + c)
a + b = n (b + c)
a = n (b + c) - b往 n (b + c) 借一个 b+c出来,有兴趣可以自己推导
a=(n-1)(b+c) + c首先 n 一定大于0,因为快指针一定比慢指针快,打个比方,就像是我和刘翔跑步,我们同时出发,我在第0圈的时候超过它是不可能的,除非我比他快,但是这就违背了那个快慢指针的设定
(快慢指针有可能在环入口相遇,但是n肯定也是大于1的,环入口相遇就是b=0,并不影响最终计算结果)
①当n=1时,a=c,把一个指针扔到初始位置,另外一个指针继续在第一次相遇点向前走(两个指针均为慢指针,都是每次走一步),刚好走c步就能到环的相遇点,最后返回结果c就行
②但是 a 比 b + c 大很多的时候(直线很长,环很短),n会很大(n>1),也就是快指针不止跑n圈,这个时候有人会犯迷糊,但是别急,还是老规矩把一个指针扔到初始位置,另外一个指针在第一次相遇点继续往前走(两个指针均为慢指针,都是每次走一步),假设现在已经走完 (n-1)(b+c) 步了,相遇点的那个指针走了 (n-1)圈又回到了相遇位置,而初始位置那个指针肯定还没走到环的起点,因为 a=(n-1)(b+c) + c > (n-1)(b+c),a走了(n-1)(b+c),也还差c步走到环的起点,是不是就跟①一样了
