文章目录

• [蓝桥杯 2021 省 A] 左孩子右兄弟
• • 题目描述
  • 输入格式
  • 输出格式
  • 样例 #1
  • • 样例输入 #1
    • 样例输出 #1
  • 提示
  • • 思路：
    • 全部代码

[蓝桥杯 2021 省 A] 左孩子右兄弟

题目描述

对于一棵多叉树，我们可以通过“左孩子右兄弟”表示法，将其转化成一棵二叉树。

如果我们认为每个结点的子结点是无序的，那么得到的二叉树可能不唯一。换句话说，每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。

给定一棵包含 NNN 个结点的多叉树，结点从 111 至 NNN 编号，其中 111 号结点是根，每个结点的父结点的编号比自己的编号小。请你计算其通过"左孩子右兄弟"表示法转化成的二叉树，高度最高是多少。（只有根结点这一个结点的树高度为 000）

例如如下的多叉树：

可能有以下 333 种 (这里只列出 333 种, 并不是全部) 不同的 “左孩子右兄弟” 表示:

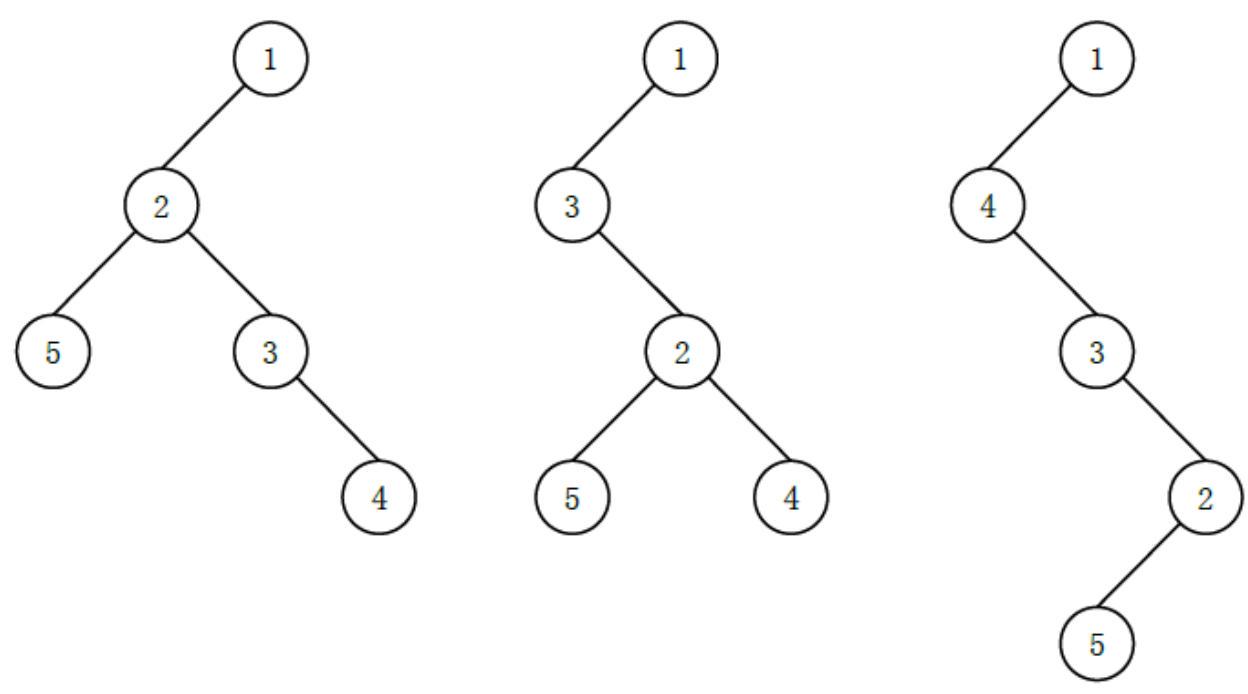
其中最后一种高度最高, 为 444。

输入格式

输入的第一行包含一个整数 NNN 。

以下 N−1N-1N−1 行, 每行包含一个整数, 依次表示 222 至 NNN 号结点的父结点编号。

输出格式

输出一个整数表示答案。

样例 #1

样例输入 #1

5
1
1
1
2

样例输出 #1

4

提示

对于 30%30 \%30% 的评测用例，1≤N≤201 \leq N \leq 201≤N≤20;

对于所有评测用例，1≤N≤1051 \leq N \leq 10^51≤N≤105 。

蓝桥杯 2021 第一轮省赛 A 组 H 题。

思路：

1.用vector来存各个节点的孩子们；

vector tree[100001];int n;cin >> n;for (int i = 2; i <= n; i++){int t;cin >> t;tree[t].push_back(i);}cout << dfs(1);

2.题目的意思就是可以让每个节点都能当左孩子然后让他的兄弟连在他的后面，而受益最大的（最深的）是什么情况呢？就是当这个孩子的数量最多的节点来当尾部节点的时候收益是最大的，我们不用考虑他怎么构成只需要知道深度，此时的最大深度：就是这一层的节点个数相加再加上孩子最多的节点的孩子数量。

3.如何找这个最大数量的节点呢？？？当然是dfs孩子节点找他的节点个数相加再加上孩子最多的节点的孩子数量；（就是递归）

int dfs(int node)
{int count = 0;if (!tree[node].size()){return 0;}for (int i = 0; i < tree[node].size(); i++){count = max(count, dfs(tree[node][i])); // 记录最大孩子}return count + tree[node].size();//return该层的深度最大是多少}

全部代码

#include 
#include using namespace std;
vector tree[100001];int dfs(int node)
{int count = 0;if (!tree[node].size()){return 0;}for (int i = 0; i < tree[node].size(); i++){count = max(count, dfs(tree[node][i])); // 记录最大孩子}return count + tree[node].size();
}int main()
{int n;cin >> n;for (int i = 2; i <= n; i++){int t;cin >> t;tree[t].push_back(i);}cout << dfs(1);system("pause");
}