目录

• 注意都是从小到大排序
• 1. 直接插入排序
• 2. 希尔排序
• 3. 选择排序
• 4. 堆排序
• 5. 冒泡排序
• 6. 快速排序
• 7. 归并排序
• 8. 基数排序(了解)
• 总结

注意都是从小到大排序

1. 直接插入排序

结合代码来理解 :

public class Test {public static void Insertsort(int[] array) {for(int i = 0; i < array.length; i++) {  //首先用i来遍历数组int tmp = array[i];      // 将i下标的元素存起来, 可以认为这样就空出一个空间来移动元素int j = 0;           //定义一个j来遍历i前面的元素for(j = i-1; j >= 0; j--) {if(array[j] > tmp) {   //如果j下标元素大于tmp, 则将j下标元素往前移一位array[j+1] = array[j];   }else {      //不大于则说明j下标及j前面的元素都小于tmp, 则退出循环(此时从0下标到j下标都已有序)break;}}array[j+1] = tmp;  //将 tmp 放到那个空出的位置上}}public static void main(String[] args) {int[] array = new int[]{4,8,1,2,9,3,20,1,5,0,22,6,21};Insertsort(array);System.out.println(Arrays.toString(array));}
}

时间复杂度计算(默认在最坏情况) : 首先 i 是从 0 开始遍历到 N 的, 当 i = 0 时, 它要比较 0 次, 当就 i 为 1 时, 就需要比较 1 次, i 为 2 时就是 2 次, 依次类推当 i 为 N 时, 就需要比较 N-1次, 由此我们列出公式(注意有N项) : 0 + 1 + 2 + 3 + 4 +…+ N-1 = N*(N-1)/2, 时间复杂度也就是O(N^2)

因为始终都是只定义一个 tmp 所以空间复杂度为O(1)

这个排序是稳定的.

我们发现当它排序越接近有序的数组时, 它的时间复杂度是越低的, 如果待排序数组是有序的话, 时间复杂度就是O(N)了. 所以元素集合越接近有序，直接插入排序算法的时间效率越高

2. 希尔排序

希尔排序法又称缩小增量法在, 它是直接插入排序的优化。
希尔排序法的基本思想是：先选定一个整数，把待排序数组的所有元素分成多个组，所有距离相同的元素分在同一组内，并对每一组内的元素进行排序。然后重复上述分组和排序的工作。当分组数到达1时，所有元素在同一组内排好序。
举个例子: 现在有个数组待排序 :

将数组分为 gap 组. 这里 gap 为 2, 对这 gap 组元素进行排序, 刚开始令 i 为 gap, 然后令 j 为 i - gap, 依次与 tmp 比较, 每次 j 都减 gap, 有序后 i++,
然后再重复上面步骤. 直到 i 遍历完数组. 然后再让 gap变小, 慢慢让多组变为一组.

public class Test {public static void Shersort(int[] array) {int gap = array.length / 2;  //gap开始时挺大的, 这样分的组多while(gap >= 1) {for(int i = gap; i < array.length; i++) {int tmp = array[i];int j = 0;for(j = i-gap; j >= 0; j -= gap) {if(array[j] > tmp) {array[j+gap] = array[j];}else {break;}}array[j+gap] = tmp;}gap /= 2;   //gap逐渐变小, 最后为1, 就是最后只有一组}}public static void main(String[] args) {int[] array = new int[]{4,8,1,2,9,3,20,1,5,0,22,6,21};Shersort(array);System.out.println(Arrays.toString(array));}
}

希尔排序特性总结:

1. 希尔排序是对直接插入排序的优化
2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。
3. 希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，我们一般认为它的时间复杂度是: O(N^1.25) 到 O(1.6*N^1.25)
4. 不稳定

3. 选择排序

这个排序就相对简单很多了, 简单来说就是每次去数组里找到最小的元素然后往前面放.

public class Test {public static void Picksort(int[] array) {for(int i = 0; i < array.length; i++) {int min = i;    //定义一个变量来记录最小元素下标, 初始为i//遍历 i 后面的元素, 当碰到比 i 下标元素小的元素时就令 min 等于该元素下标for(int j = i+1; j < array.length; j++) {  if(array[min] > array[j]) {min = j;}}//最后将 i 指向的元素与找到的最小元素交换位置int tmp = array[i];array[i] = array[min];array[min] = tmp;}}public static void main(String[] args) {int[] array = new int[]{6,10,3,4,1,2,0,5,9,7,8};Picksort(array);System.out.println(Arrays.toString(array));}
}

选择排序特性总结 :

1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

4. 堆排序

堆排序首先就是将待排序数组建为大根堆(排升序用大根堆), 然后我们就得到了最大元素, 将最大元素与最后一个元素交换位置, 这样最大的元素就排好了, 然后再剩下的元素重复上面操作即可.

public class Test {public static void Heapsort(int[] array) {Heap(array);   //建立大根堆for(int i = array.length-1; i > 0; i--) {//将最大元素与最后的元素互换int tmp = array[0];array[0] = array[i];array[i] = tmp;//换完了再向下调整, 又变为大根堆, 堆的长度要减一func(array,0,i);}}//建立大根堆, 建堆的时间复杂度: O(N)private static void Heap(int[] array) {int len = array.length;for(int i = (len-1-1)/2; i >= 0; i--) {func(array,i,len);  //从最后一个拥有孩子节点的树开始依次向下调整}}//向下调整, 时间复杂度: O(logN)private static void func(int[] array, int r, int len) {int a = 2*r;while(a < len) {//找出最大的子节点if(a+1 < len && array[a] < array[a+1]) {a = a+1;   }//与父节点比较, 若比父节点大, 则交换, 否则调整完毕退出循环if(array[a] > array[r]) {int tmp = array[a];array[a] = array[r];array[r] = tmp;//令r指向交换了的孩子节点, 继续循环r = a;a = 2*r;}else {break;}}}public static void main(String[] args) {int[] array = new int[]{6,10,3,4,1,2,0,5,9,7,8};Heapsort(array);System.out.println(Arrays.toString(array));}
}

堆排序的特性总结 :

1. 时间复杂度：O(N*logN)
2. 空间复杂度：O(1)
3. 稳定性：不稳定

5. 冒泡排序

这个相信大家都不陌生了.

public class Test {public static void Bubble(int[] array) {for(int i = 0; i < array.length-1; i++) { for(int j = 0; j < array.length-1-i; j++) {if(array[j] > array[j+1]) {int tmp = array[j];array[j] = array[j+1];array[j+1] = tmp;}}}}public static void main(String[] args) {int[] array = new int[]{6,10,3,4,1,2,0,5,9,7,8};Bubble(array);System.out.println(Arrays.toString(array));}
}

我们还可以给它优化一下:

public class Test {public static void Bubble(int[] array) {for(int i = 0; i < array.length-1; i++) {int m = 0;   //定义 m, 如果本次 j 进行的for循环没有改变元素位置, 则说明已经有序直接返回for(int j = 0; j < array.length-1-i; j++) {if(array[j] > array[j+1]) {int tmp = array[j];array[j] = array[j+1];array[j+1] = tmp;m = 1;}}if(m == 0) {return;}}}
}

冒泡排序的特性总结:

1. 时间复杂度：O(N^2)
2. 空间复杂度：O(1)
3. 稳定性：稳定

6. 快速排序

快速排序有几种写法, 我们这就列举相对简单的 Hoare 法:
任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后将左右子序列重复该过程，直到所有元素都排列在相应位置上为止.
我们可以直接将最左边元素作为基准值来分割序列, 定义 l 和 r 分别代表该序列最左边与最右边位置下标, 先从右边开始往后找到比 6 小的元素下标, 再从左边开始找到比 6 大的元素下标, 然后将它两元素交换, 继续上述操作, 直到它两相遇, 然后交换基准值与相遇位置元素, 然后将 6 左边数组与右边数组重复上面操作.

public class Test {public static void Sort(int[] array){int left = 0;int right = array.length-1;SortChild(array,left,right);}private static void SortChild(int[] array, int left, int right) {if(left >= right) {  //结束递归条件return;}int l = left;int r = right;int key = array[l];  //记录基准值while(l < r) {while(l < r && array[r] >= key) {  //注意找的是小于key的值, 得加等于号, 下面同理r--;  }while(l < r && array[l] <= key) {l++;}Swap(array,l,r);  //找到后交换元素}Swap(array,left,l);  //最后把key与相遇下标值交换SortChild(array,left,l-1);SortChild(array,l+1,right);}public static void Sort(int[] array){int left = 0;int right = array.length-1;SortChild(array,left,right);}
}

理想情况下, 它是类似与二叉树结构 , 每层都是比较 N 次, 那高度是 lgN, 时间复杂度就是N*lgN.
但这是理想情况, 如果我们给的是一个有序数组呢?
那它每层比较 N 次, 但它的高度却是 N, 所以时间复杂度为 N^2.
我们可以对它进行优化, 就是用三数取中法, 来取出首尾中三元素的中间值, 然后将中间值与首元素交换, 作为基准, 再来排序.

快速排序总结:

1. 快速排序整体的综合性能和使用场景都是比较好的.
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(logN)
4. 稳定性：不稳定

7. 归并排序

归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

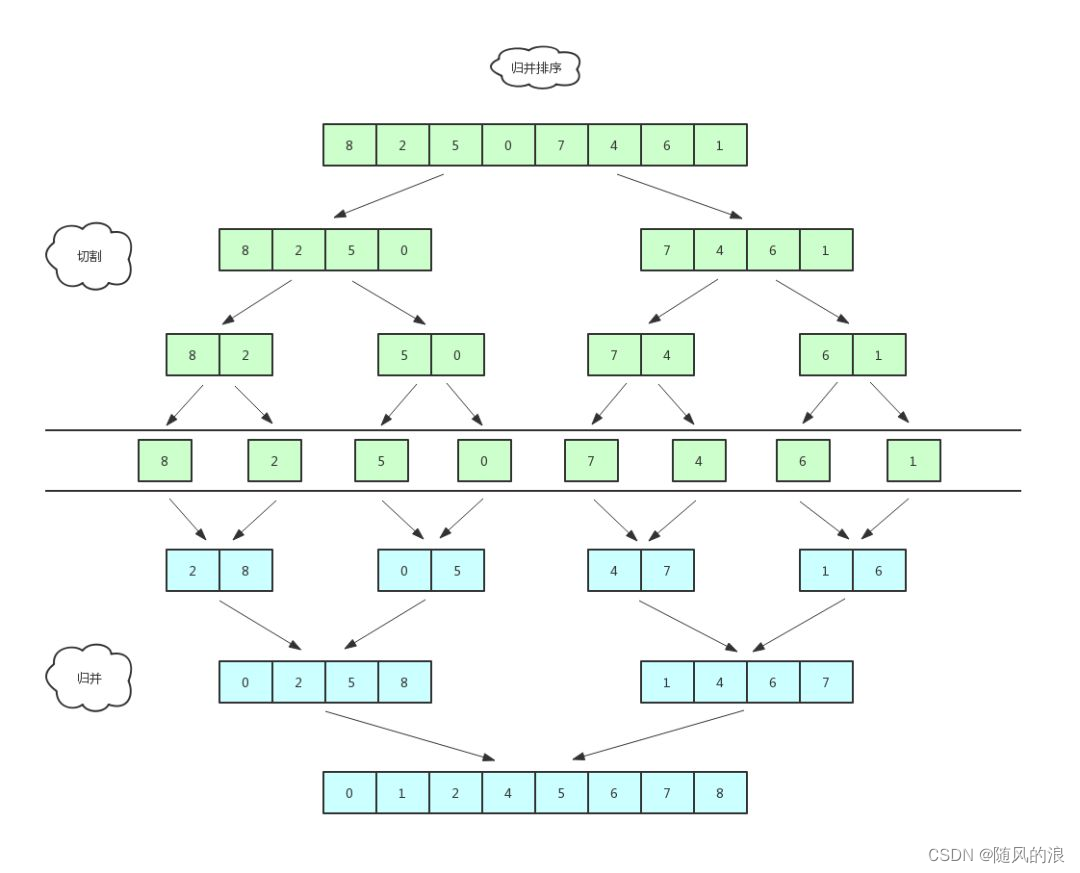
public class Test {public static void Merge(int[] array) {MergeChild(array,0,array.length-1);}private static void MergeChild(int[] array, int left, int right) {if(left >= right) {   //递归结束条件return;}int m = (left+right)/2;MergeChild(array,left,m);  //往左递归MergeChild(array,m+1,right);  //往右递归//将两个子序列合并int a = left;int b = m+1;int size = right-left+1;int[] arr = new int[size];   //定义一个数组存放两个子序列int j = 0; //将两个子序列有序放入arr数组中while(a <= m && b <= right) {if(array[a] < array[b]) {arr[j++] = array[a++];}else {arr[j++] = array[b++];}}if(a > m) {while(b <= right) {arr[j++] = array[b++];}}else {while(a <= m) {arr[j++] = array[a++];}}//将arr数组元素重新放入array数组中for(int i = 0; i < size; i++) {array[i+left] = arr[i];}}
}

归并排序总结:

1. 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(N)
4. 稳定性：稳定

8. 基数排序(了解)

思想：计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。
操作步骤：

1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中

public class Test {public static void Radix(int[] array) {int min = array[0];int max = array[0];//找出最大与最小值for(int i = 1; i < array.length; i++) {if(array[i] < min) {min = array[i];}if(array[i] > max) {max = array[i];}}//创建一个元素大小范围的数组int[] arr = new int[max-min+1];//用该数组记录下标为 array[i]-min 的元素个数for(int i = 0; i < array.length; i++) {arr[array[i]-min]++;}int j = 0;   // j记录赋值时array的下标//将记录的数据记录进原数组for(int i = 0; i < arr.length; i++) {while(arr[i] != 0) {   //根据arr[i]记录的个数来决定赋值次数array[j++] = i+min;  //i+m是利用i将原来元素的大小翻译出来arr[i]--;}}}
}

计数排序的特性总结:

1. 计数排序在数据范围集中时，效率很高，但是适用范围及场景有限。
2. 时间复杂度：O(MAX(N,范围))
3. 空间复杂度：O(范围)
4. 稳定性：稳定

总结

上述八大排序中, 稳定的排序仅三个 : 直接插入排序, 冒泡排序, 归并排序.
基数排序算不上稳定, 因为它存放的数据都不是原来的数据了.