【C++】面试101,二叉搜索树的最近公共祖先,在二叉树中找到两个节点的最近公共祖先,序列化二叉树,重建二叉树,输出二叉树的右视图,组队竞赛,删除公共字符
目录
1.二叉搜索树的最近公共祖先
2.在二叉树中找到两个节点的最近公共祖先
3.序列化二叉树
4.重建二叉树
5.输出二叉树的右视图
6.组队竞赛
7.删除公共字符
1.二叉搜索树的最近公共祖先
这是一个简单的问题,因为是二叉搜索树(有序),首先看看p,q是不是都在左子树?右子树
如果不是,那么现在的根就是两个的最近公共祖先
int lowestCommonAncestor(TreeNode* root, int p, int q) {// write code here、if(!root) return -1;if(pval &&qval) return lowestCommonAncestor(root->left, p, q);else if(p>root->val && q>root->val) return lowestCommonAncestor(root->right, p, q);//在两个子树else return root->val;} 2.在二叉树中找到两个节点的最近公共祖先
最一般的树怎么找最近公共祖先?
最直观的方法肯定是和上面搜索树的想法一样,先看看这两个节点是不是在一侧的子树里
但是这不是搜索树,不可以比较节点的值来判断在左子树/右子树
没有条件创造条件也要上,谁让我想不出来更好的思路....

bool Isintree(TreeNode* root, int x) {if (!root) return false;return root->val == x||Isintree(root->left, x) ||Isintree(root->right, x);}int lowestCommonAncestor(TreeNode* root, int o1, int o2) {if (!root) return -1;if (root->val == o1 || root->val == o2) return root->val;bool Iso1inleft = Isintree(root->left, o1);bool Iso1inright = !Iso1inleft;bool Iso2inleft = Isintree(root->left, o2);bool Iso2inright = !Iso2inleft;if ((Iso1inleft && Iso2inright) || (Iso1inright && Iso2inleft))return root->val;if (Iso1inleft && Iso2inleft)return lowestCommonAncestor(root->left, o1, o2);elsereturn lowestCommonAncestor(root->right, o1, o2);}欣喜若狂的提交,超时!!!!!!!!!!!!!!!!!!!!!!!!!!!!
为什么?
因为在子树里搜索很浪费时间
那么只能换方法
记得我们怎么做相交链表的题目吗?
想找到链表的交点,那么我们计算两个链表的长度,让更长的链表先走差距(两个链表长度差)步,然后挨个比较目前的val值,找到一样的就输出
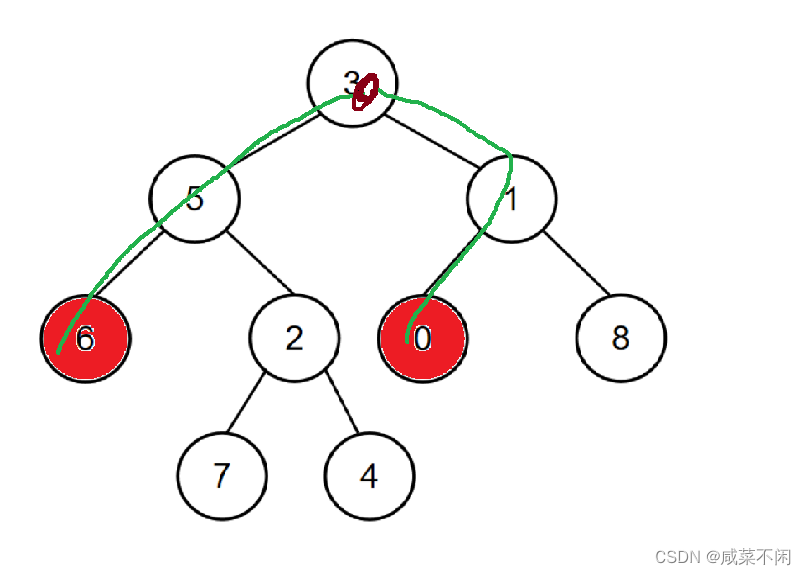
那你看这个树枝是不是很像链表
所以思路就有了
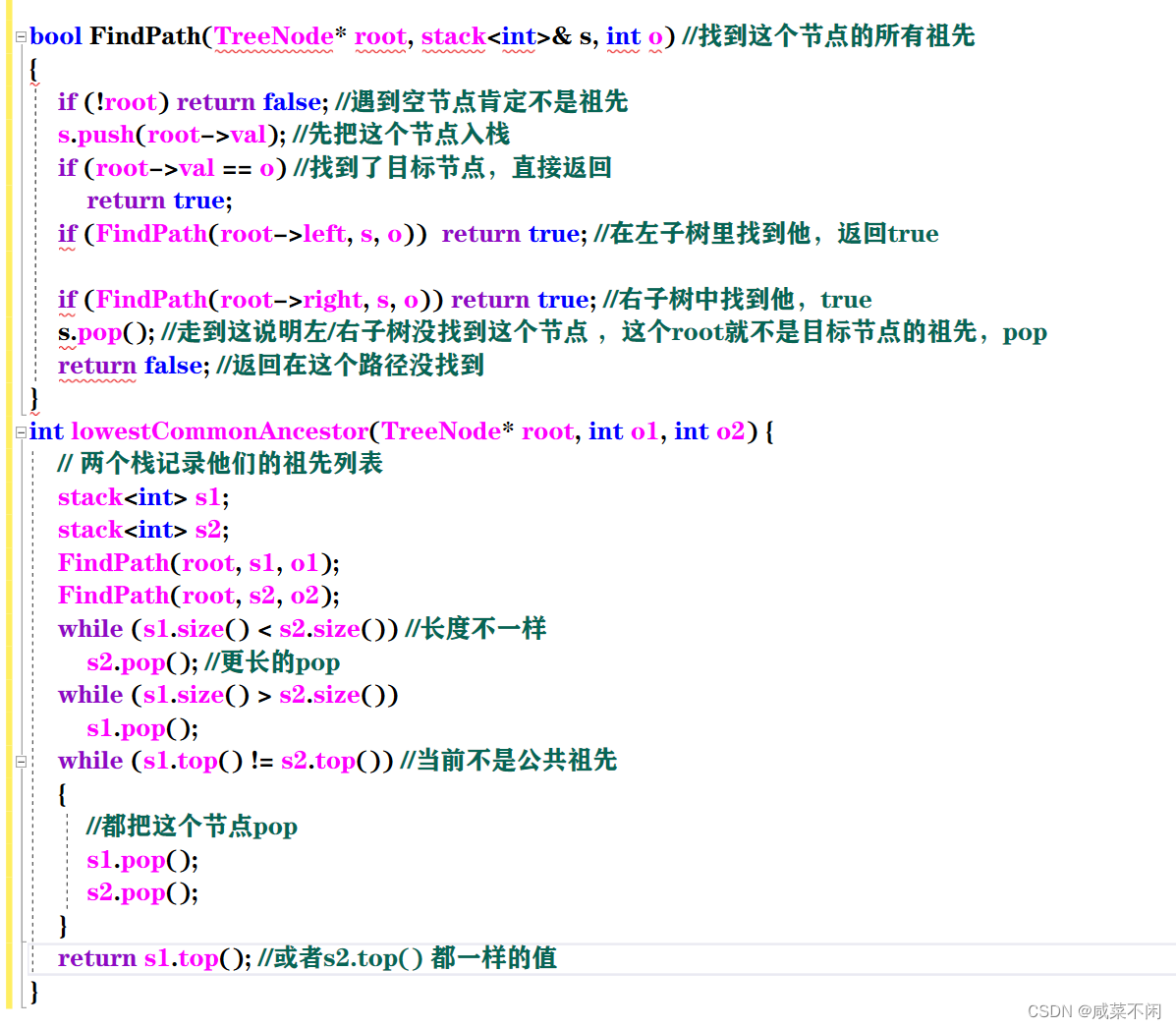
bool FindPath(TreeNode* root, stack& s, int o) //找到这个节点的所有祖先
{if (!root) return false; //遇到空节点肯定不是祖先s.push(root->val); //先把这个节点入栈if (root->val == o) //找到了目标节点,直接返回return true;if (FindPath(root->left, s, o)) return true; //在左子树里找到他,返回trueif (FindPath(root->right, s, o)) return true; //右子树中找到他,trues.pop(); //走到这说明左/右子树没找到这个节点 ,这个root就不是目标节点的祖先,popreturn false; //返回在这个路径没找到
}
int lowestCommonAncestor(TreeNode* root, int o1, int o2) {// 两个栈记录他们的祖先列表stack s1;stack s2;FindPath(root, s1, o1);FindPath(root, s2, o2);while (s1.size() < s2.size()) //长度不一样s2.pop(); //更长的popwhile (s1.size() > s2.size())s1.pop();while (s1.top() != s2.top()) //当前不是公共祖先 {//都把这个节点pops1.pop();s2.pop();}return s1.top(); //或者s2.top() 都一样的值
} 3.序列化二叉树
写两个函数,让字符串可以构建成二叉树,二叉树也可以写成字符串

void dfs_Serialize(TreeNode* root, string& s)
{if (!root)//如果是空节点,直接写一个#,空节点的子节点被省略,所以直接返回{s += '#';return;}s += to_string(root->val) + ','; //把非空节点的val变成字符,写入到字符串dfs_Serialize(root->left, s); //左子树dfs_Serialize(root->right, s);//右子树
}
char* Serialize(TreeNode* root) { //用二叉树写字符串数组string s; //首先写成字符串dfs_Serialize(root, s); //深度优先遍历(前序)char* ans = new char[s.size() + 1]; //最后应该输出数组形式,先开数组(加上1写'\0')memcpy(ans, s.c_str(), s.size()); //把字符串拷贝给数组ans[s.size()] = '\0';//终止符return ans;
}
TreeNode* dfs_Deserialize(char*& s) //把字符串变二叉树,注意这个字符串在递归的时候不是每次从头开始,所以&
{if (*s == '#')//是空节点的标志,直接返回nullptr{s++; //s向后走一个,因为这个字符对应的节点已经被表示完了return nullptr;}int val = 0; //字符串对应的节点valwhile (*s != ',') //看样例,字符串以,分割{val = val * 10 + (*s - '0'); //万一不是个位数,需要这样算好每一位s++;//s往后走}s++; //把逗号跳过TreeNode* root = new TreeNode(val); //用val创建节点root->left = dfs_Deserialize(s); //左节点的创建root->right = dfs_Deserialize(s);//右节点return root; //返回根
}
TreeNode* Deserialize(char* str) {return dfs_Deserialize(str);
}还有第二个方法,借助队列,把字符串构建成二叉树(这个显然没有上面的方法快)

char* Serialize(TreeNode* root) { //用层序来写字符串if (!root) return nullptr; //如果是空节点,不需要记录他的孩子string str; queue que;que.push(root); //先把根入队while (!que.empty()){auto node = que.front(); //取队头元素que.pop();if (node) //取出的节点不是空{str += to_string(node->val) + ","; //字符串保存这个节点val对应的字符,并且在字符串里面写入分割符号que.push(node->left);//带入左孩子que.push(node->right);}else {str += "#";//是空,写成#}}auto res = new char[str.size() + 1]; //和上一方法这里的用处一样strcpy(res, str.c_str());res[str.size()] = '\0';return res;
}
int Getinteger(char* str, int& k) //把字符转化成数字
{int val = 0;while (str[k] != ',' && str[k] != '\0' && str[k] != '#'){val = val * 10 + str[k] - '0';++k;}if (str[k] == '\0') return -1;if (str[k] == '#') val = -1;k++;return val;
}
TreeNode* Deserialize(char* str) {if (!str) return nullptr;int k = 0; //记录字符串的下标queue que;auto head = new TreeNode(Getinteger(str, k)); //一定要把字符串下标也传,要不然找不到位置了que.push(head); //把头结点入队while (!que.empty()){auto node = que.front();//队头que.pop();//这里的反序列化是根据前序用字符串构建二叉树int leftval = Getinteger(str, k); //把字符串转换成左节点的valif (leftval != -1)//如果左孩子的val是-1,代表是空节点{//不是空auto nodeleft = new TreeNode(leftval) ;//创建节点node->left = nodeleft; //node和左孩子链接que.push(nodeleft);//链接好的节点入队}//右节点同样的方法int rightval = Getinteger(str, k);if (rightval != -1){auto noderight = new TreeNode(rightval);node->right = noderight;que.push(noderight);}}return head; //返回头结点
} 4.重建二叉树
之前就说过三种遍历方式:前中后,只有前+后不能构建出二叉树
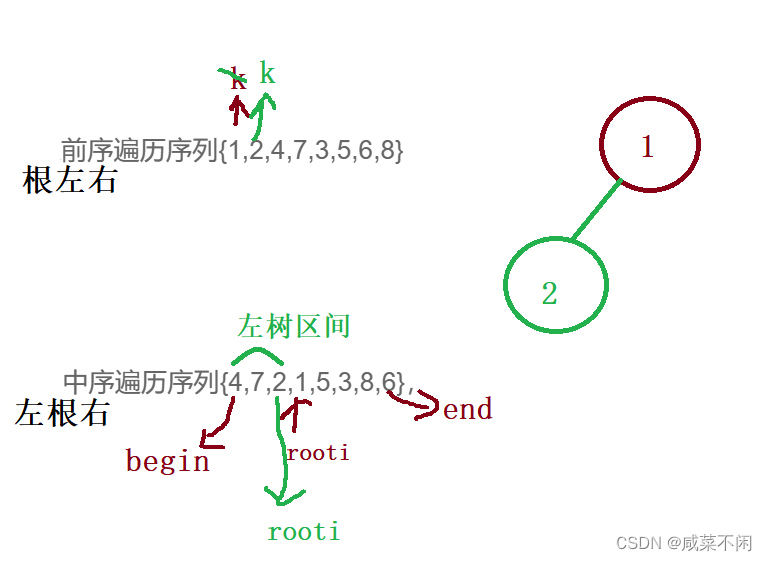
同一个颜色是同一次递归
最后根据 这个规律可以得到二叉树
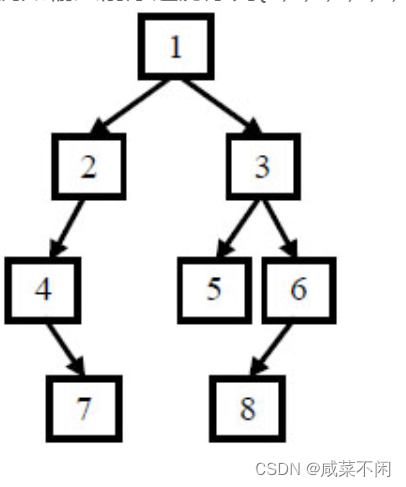

TreeNode* _reConstructBinaryTree(vector& pre, vector& vin, int& k, //k一定要给&,在每个递归里是看得见改变的int begin, int end) {if (begin > end) return nullptr; //区间不成立,说明为空int rooti = begin; //rooti记录中序节点里面根的下标while (rooti <= end) { //根的下标肯定在合法区间里if (vin[rooti] == pre[k]) //在中序数组里找到根,k记录每个根在前序里的下标break;++rooti;}//rooti代表根节点的下标//[begin,rooti-1] rooti [rooti+1,end]TreeNode* root = new TreeNode(pre[k++]); //创建节点root->left =_reConstructBinaryTree(pre, vin, k, begin, rooti - 1); //左孩子在左区间找(因为中序是左根右)root->right =_reConstructBinaryTree(pre, vin, k, rooti + 1, end);return root;
}
TreeNode* reConstructBinaryTree(vector pre, vector vin) {int k = 0;return _reConstructBinaryTree(pre, vin, k, 0, pre.size() - 1);
} 5.输出二叉树的右视图
根据给的前序和中序构建树,然后层序思想,每次到一层的最左侧,直接入ans

TreeNode* buildtree(vector& xianxu, vector& zhongxu, int& k, //建树(和前面重建二叉树是一样的)int begin, int end) {if (begin > end) return nullptr;int rooti = begin;while (rooti <= end) {if (xianxu[k] == zhongxu[rooti])break;++rooti;}TreeNode* root = new TreeNode(xianxu[k++]);root->left = buildtree(xianxu, zhongxu, k, begin, rooti - 1);root->right = buildtree(xianxu, zhongxu, k, rooti + 1, end);return root;
}
void bfs(TreeNode* root, vector& ans) { //层序+找最右节点if (!root) return;queue q;q.push(root);while (!q.empty()) {int size = q.size(); //当前层数的sizewhile (size--) {TreeNode* node = q.front();q.pop();if (size == 0) ans.push_back(node->val); //直到size==0,找到最右节点if (node->left) q.push(node->left);if (node->right) q.push(node->right);}}
}
vector solve(vector& xianxu, vector& zhongxu) {// write code herevector ans;int k = 0;TreeNode* root = buildtree(xianxu, zhongxu, k, 0, xianxu.size() - 1);bfs(root, ans);return ans;
}
但是这样做总是觉得很麻烦,所以去评论区看来一下大佬的代码

void _solve(vector xianxu, vector zhongxu, vector& ans,int level) {if (xianxu.empty()) return; //如果前序是空的,证明根是空if (ans.size() < level) ans.push_back(xianxu[0]); //ans里面的元素个数一定是等于层数,如果小于,直接把当前的根入elseans[level - 1] = xianxu[0]; //level应该也是ans的个数,最后一个元素下标就是level-1int headpos = 0; //还是找中序里的根while (zhongxu[headpos] != xianxu[0])headpos++;_solve(vector(xianxu.begin() + 1, xianxu.begin() + headpos + 1), vector(zhongxu.begin(), zhongxu.begin() + headpos), ans, level + 1);_solve(vector(xianxu.begin() + headpos + 1, xianxu.end()),vector(zhongxu.begin() + headpos + 1, zhongxu.end()), ans, level + 1);
}
vector solve(vector& xianxu, vector& zhongxu) {vector ans;_solve(xianxu, zhongxu, ans, 1);return ans;
} 前面的不解释了,主要看大佬的递归
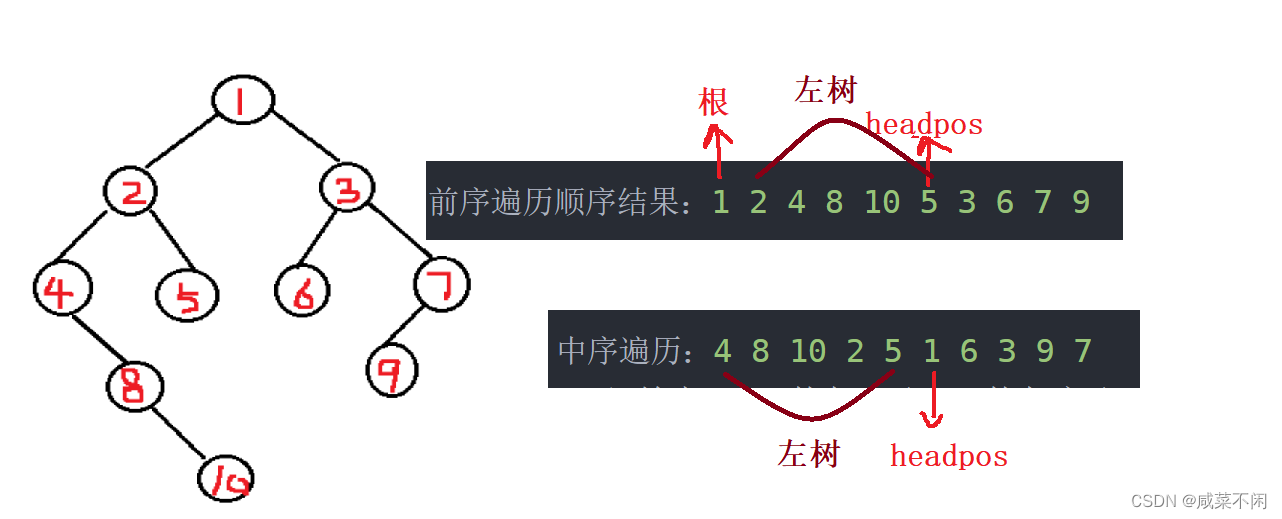
之前我们构建二叉树的时候只想着找到根节点的下标,但是居然没有发现前序begin()+1~begin()+headpos整个闭区间是左子树的所有节点!!!!!!!!!!!!!!!
也就是说我们之前写的构造二叉树的所有步骤都写麻烦了
来看前序+中序怎么构建二叉树
TreeNode* _reConstructBinaryTree(vector pre, vectorvin) {if (pre.empty()) return nullptr;int rooti = 0;while (vin[rooti] != pre[0]) {++rooti;}TreeNode* root = new TreeNode(pre[0]);root->left =_reConstructBinaryTree(vector(pre.begin() + 1, pre.begin() + rooti + 1),vector(vin.begin(), vin.begin() + rooti));root->right =_reConstructBinaryTree(vector(pre.begin() + 1 + rooti, pre.end()),vector(vin.begin() + rooti + 1, vin.end()));return root;
}
TreeNode* reConstructBinaryTree(vector pre, vector vin) {return _reConstructBinaryTree(pre, vin);
} 6.组队竞赛
这个题不在面试必刷101,作为补充
一道简单的数学题
其实没啥好说的,先排序,最小的节点就是前n个,n是队伍的个数,也就代表了如果想让所有队伍的能力值和最大,必须每个队伍有一个重排v之后的前n个数之一
比如

n=2
排序之后前两个数1 2,应该给每个队伍分配一个,不能让1 2同时出现在一个队伍里
所以sum求和的时候i从n开始,不应该直接挨着取n之后的元素,因为你把最大的一些数全部没取到,应该跳两个取一次
#include
#include
#include
using namespace std;
int main()
{int n;while (cin >> n){vector v;v.resize(3 * n);for (int i = 0; i < v.size(); i++){cin >> v[i];}sort(v.begin(), v.end());long long sum = 0;for (int i = n;i < v.size(); i += 2){sum += v[i];}cout << sum< 7.删除公共字符
#include
#include using namespace std;int main(){string s1, s2;getline(cin, s1);getline(cin, s2);for (int i= 0; i < s1.size(); i++) {if (s2.find(s1[i]) == -1) //在s2中找不到这个字符则输出cout << s1[i];}return 0;} 这个不是我自己最初写的,一开始是把s2里面先遍历然后映射到数组里,但是显然慢
这个直接在s2里面找s1是不是在很方便
