题目

面试题13. 机器人的运动范围【中等】

题解

机器人每次只能移动一格，因此每次只需计算 x 到 x±1 的数位和增量。

数位和增量公式：设x的数位和sxs_xsx​，x的数位和sx+1s_{x+1}sx+1​

1. 当 (x+1)%10=0 时：sx+1=sx−8s_{x+1}=s_x-8sx+1​=sx​−8，例如19数位和10，20数位和2；
2. 当 (x+1)%10≠0 时：sx+1=sx+1s_{x+1}=s_x+1sx+1​=sx​+1，例如1数位和1，2数位和2。

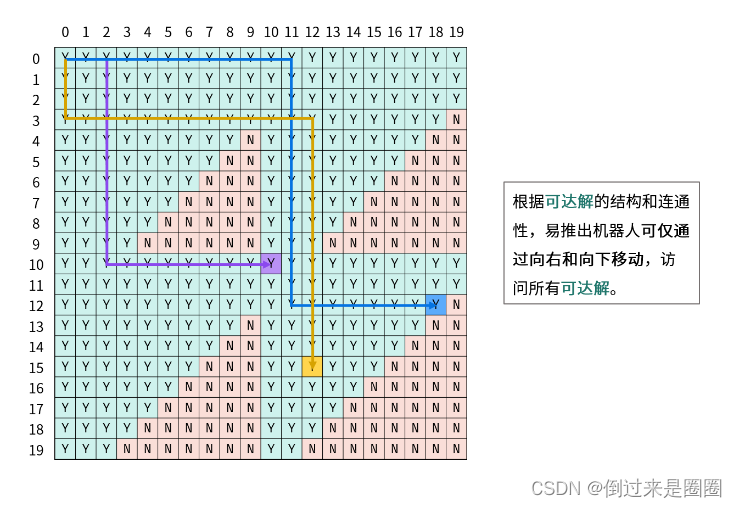
可达解分析：根据数位和增量公式得知，数位和每逢进位突变一次。
因此可以将矩阵分为三个区域，黄色三角形区域内的解虽然满足数位和要求，但由于机器人每步只能走一个单元格，而三角形间不一定是连通的，因此机器人不一定能到达，称为不可达解。可到达的称为可达解。

根据可达解的结构和连通性，易推出机器人可仅通过向右和向下移动，访问所有可达解。

• 三角形内部： 全部连通；
• 两三角形连通处： 若某三角形内的解为可达解，则必与其左边或上边的三角形连通（即相交），即机器人必可从左边或者上边走进此三角形。

DFS

• 递归参数：当前元素索引行 i 列 j ，两者的数位和si，sj
• 终止条件：当 行列索引越界 or 数位和超出目标值k or 当前元素已访问过 时，返回0，不计入可达解。
• 递推工作：
  1.标记当前单元格：（i，j）存入Set visited 中，代表此单元格已被访问过。
  2.搜索下一单元格：计算当前元素的 下、右 两个方向元素的数位和，并开启下层递归。
• 回溯返回值：返回 1+右方搜索可达解总数+下方搜索可达解总数 ，代表从本单元格递归搜索的可达解总数。

class Solution {int row,col,lim;boolean[][] visited;public int movingCount(int m, int n, int k) {row=m;col=n;lim=k;visited=new boolean[m][n];return dfs(0,0,0,0);}public int dfs(int i,int j,int si,int sj){if(i>=row||j>=col||si+sj>lim||visited[i][j])return 0;visited[i][j]=true;int newSi=(i+1)%10==0?si-8:si+1;//(i+1,j)数位和int newSj=(j+1)%10==0?sj-8:sj+1;//(i,j+1)数位和return 1+dfs(i+1,j,newSi,sj)+dfs(i,j+1,si,newSj);}
}

时间复杂度：O(mn)O(mn)O(mn)

空间复杂度：O(mn)O(mn)O(mn)

BFS

• 初始化：初始点(0,0)加入队列queue；
• 迭代终止条件：队列为空，表示已遍历完所有可达解。
• 迭代工作：
  1.单元格出队：队首单元格的 索引、数位和 弹出，作为当前搜索单元格。
  2.判断是否跳过：若 行列索引越界 or 数位和超过目标值k or 当前元素已访问过 时，执行continue。
  3.标记当前单元格：将单元格索引（i，j）存入Set visited 中，代表此单元格已被访问过。
  4.单元格入队：将当前元素的 下方、右方 单元格的索引、数位和加入queue。
• 返回值：Set visited 的长度，即可达解的数量。

class Solution {public int movingCount(int m, int n, int k) {boolean[][] visited=new boolean[m][n];int res=0;Queuequeue=new LinkedList<>();queue.offer(new int[]{0,0,0,0});while(!queue.isEmpty()){int[] x=queue.poll();int i=x[0],j=x[1],si=x[2],sj=x[3];if(i>=m||j>=n||si+sj>k||visited[i][j])continue;visited[i][j]=true;res++;int newSi=(i+1)%10==0?si-8:si+1;int newSj=(j+1)%10==0?sj-8:sj+1;queue.offer(new int[]{i+1,j,newSi,sj});queue.offer(new int[]{i,j+1,si,newSj});}return res;}
}

时间复杂度：O(mn)O(mn)O(mn)

空间复杂度：O(mn)O(mn)O(mn)