线段树——懒标记下放
【模板】线段树 1
题目描述
如题,已知一个数列,你需要进行下面两种操作:
- 将某区间每一个数加上 kkk。
- 求出某区间每一个数的和。
输入格式
第一行包含两个整数 n,mn, mn,m,分别表示该数列数字的个数和操作的总个数。
第二行包含 nnn 个用空格分隔的整数,其中第 iii 个数字表示数列第 iii 项的初始值。
接下来 mmm 行每行包含 333 或 444 个整数,表示一个操作,具体如下:
1 x y k:将区间 [x,y][x, y][x,y] 内每个数加上 kkk。2 x y:输出区间 [x,y][x, y][x,y] 内每个数的和。
输出格式
输出包含若干行整数,即为所有操作 2 的结果。
样例 #1
样例输入 #1
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4
样例输出 #1
11
8
20
提示
对于 30%30\%30% 的数据:n≤8n \le 8n≤8,m≤10m \le 10m≤10。
对于 70%70\%70% 的数据:n≤103n \le {10}^3n≤103,m≤104m \le {10}^4m≤104。
对于 100%100\%100% 的数据:1≤n,m≤1051 \le n, m \le {10}^51≤n,m≤105。
保证任意时刻数列中所有元素的绝对值之和 ≤1018\le {10}^{18}≤1018。
【样例解释】
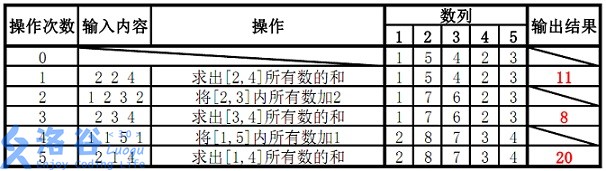
懒标记用于计算每个线段的变化程度,在这题就是每个线段增加的数之和,当我们的add操作和query操作都没有遍历到所输入的x y的时候,我们就需要不断的把懒标记进行下放,下放完之后我们还得记得维护f的值,使其不失真,具体看代码
#include
#define ll long long
using namespace std;
ll f[400005],v[400005];
int n,m,a[100005];
inline void buildtree(int k,int l,int r){if(l==r){f[k]=a[l];return;}int mid=(l+r)>>1;buildtree(k<<1,l,mid);buildtree(k<<1|1,mid+1,r);f[k]=f[k<<1]+f[k<<1|1];
}
inline void push_down(int k){//将懒标记点下放v[k<<1]+=v[k],v[k<<1|1]+=v[k],v[k]=0;
}
inline void push_up(int k,int l,int r,int m){//维护f[k]的值,使其不失真f[k]=f[k<<1]+v[k<<1]*(m-l+1)+f[k<<1|1]+v[k<<1|1]*(r-m);
}
inline void add(int k,int l,int r,int x,int y,int num){if(l==x&&r==y){v[k]+=num;return;}if(v[k])push_down(k);int mid=(l+r)>>1;if(y<=mid)add(k<<1,l,mid,x,y,num);elseif(x>mid)add(k<<1|1,mid+1,r,x,y,num);else add(k<<1,l,mid,x,mid,num),add(k<<1|1,mid+1,r,mid+1,y,num);push_up(k,l,r,mid);
}
inline ll query(int k,int l,int r,int x,int y){if(l==x&&r==y)return f[k]+v[k]*(r-l+1);if(v[k])push_down(k);int mid=(l+r)>>1;ll res;if(y<=mid)res=query(k<<1,l,mid,x,y);elseif(x>mid)res=query(k<<1|1,mid+1,r,x,y);else res=query(k<<1,l,mid,x,mid)+query(k<<1|1,mid+1,r,mid+1,y);push_up(k,l,r,mid);return res;
}
int main(){cin>>n>>m;for(int i=1;i<=n;++i)scanf("%d",&a[i]);buildtree(1,1,n);while(m--){int t,x,y,num;scanf("%d%d%d",&t,&x,&y);if(t==1){scanf("%d",&num);add(1,1,n,x,y,num);}else cout< 【模板】线段树 2
题目描述
如题,已知一个数列,你需要进行下面三种操作:
-
将某区间每一个数乘上 xxx
-
将某区间每一个数加上 xxx
-
求出某区间每一个数的和
输入格式
第一行包含三个整数 n,m,pn,m,pn,m,p,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含 nnn 个用空格分隔的整数,其中第 iii 个数字表示数列第 iii 项的初始值。
接下来 mmm 行每行包含若干个整数,表示一个操作,具体如下:
操作 111: 格式:1 x y k 含义:将区间 [x,y][x,y][x,y] 内每个数乘上 kkk
操作 222: 格式:2 x y k 含义:将区间 [x,y][x,y][x,y] 内每个数加上 kkk
操作 333: 格式:3 x y 含义:输出区间 [x,y][x,y][x,y] 内每个数的和对 ppp 取模所得的结果
输出格式
输出包含若干行整数,即为所有操作 333 的结果。
样例 #1
样例输入 #1
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4
样例输出 #1
17
2
提示
【数据范围】
对于 30%30\%30% 的数据:n≤8n \le 8n≤8,m≤10m \le 10m≤10
对于 70%70\%70% 的数据:$n \le 10^3 ,,, m \le 10^4$
对于 100%100\%100% 的数据:$ n \le 10^5,,, m \le 10^5$
除样例外,p=571373p = 571373p=571373
(数据已经过加强_)
样例说明:
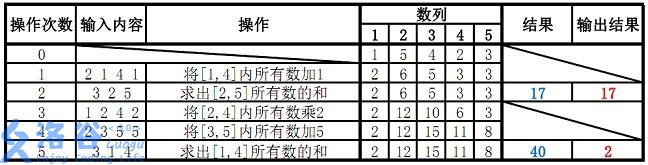
故输出应为 171717、222( 40mod38=240 \bmod 38 = 240mod38=2 )
对于这道题,我们首先能确认懒标记应该要有两个,因为对于add而言,懒标记的初始值应该为0,而对于mul而言,懒标记的初始值应该为1,两者肯定不可能是同一个懒标记。
但是对于懒标记mul,初始化起来比较复杂,因此最好的方式就是就是在建树的时候初始化为1,这时候构造结构体的必要性就有了。
下放需要有个规则,首先,下放的时候对于add而言,应该乘以父亲结点的mul,再加上父亲结点的add;对于mul而言,直接乘以父亲结点的mul即可;对于val而言,其等于自己原本的val父亲的mul再加上线段长度父亲的add,说起来有点绕,具体看代码即可
#include
#define ll long long
using namespace std;
const int N=1e5+5;
int n,m,p,a[N];
struct node{ll val,add,mul;int len;
}t[4*N];
inline void buildtree(int k,int l,int r){t[k].add=0,t[k].mul=1;t[k].len=(r-l+1);if(l==r){t[k].val=a[l];return;}int mid=(l+r)>>1;buildtree(k<<1,l,mid),buildtree(k<<1|1,mid+1,r);t[k].val=(t[k<<1].val+t[k<<1|1].val)%p;
}
inline void push_down(int k){t[k<<1].add=(t[k<<1].add*t[k].mul+t[k].add)%p;t[k<<1].mul=(t[k<<1].mul*t[k].mul)%p;t[k<<1].val=t[k<<1].val*t[k].mul%p+t[k<<1].len*t[k].add%p;t[k<<1|1].add=(t[k<<1|1].add*t[k].mul+t[k].add)%p;t[k<<1|1].mul=t[k<<1|1].mul*t[k].mul%p;t[k<<1|1].val=t[k<<1|1].val*t[k].mul%p+t[k<<1|1].len*t[k].add%p;t[k].mul=1,t[k].add=0;
}
inline void push_up(int k){t[k].val=(t[k<<1].val+t[k<<1|1].val)%p;
}
inline void modify(int k,int l,int r,int x,int y,int add,int mul){if(l==x&&y==r){t[k].val=(t[k].val*mul%p+t[k].len*add)%p;t[k].mul=t[k].mul*mul%p;t[k].add=(t[k].add*mul%p+add)%p;return;}if(t[k].add!=0||t[k].mul!=1)push_down(k);int mid=(l+r)>>1;if(y<=mid)modify(k<<1,l,mid,x,y,add,mul);elseif(x>mid)modify(k<<1|1,mid+1,r,x,y,add,mul);else modify(k<<1,l,mid,x,mid,add,mul),modify(k<<1|1,mid+1,r,mid+1,y,add,mul);push_up(k);
}
inline ll query(int k,int l,int r,int x,int y){if(l==x&&r==y)return t[k].val;if(t[k].add!=0||t[k].mul!=1)push_down(k);int mid=(l+r)>>1;ll res;if(y<=mid)res=query(k<<1,l,mid,x,y);elseif(x>mid)res=query(k<<1|1,mid+1,r,x,y);else res=(query(k<<1,l,mid,x,mid)+query(k<<1|1,mid+1,r,mid+1,y))%p;return res;
}
int main(){cin>>n>>m>>p;for(int i=1;i<=n;++i)scanf("%d",&a[i]);buildtree(1,1,n);while(m--){int c,x,y,k;scanf("%d%d%d",&c,&x,&y);if(c==1){scanf("%d",&k);modify(1,1,n,x,y,0,k);}else if(c==2){scanf("%d",&k);modify(1,1,n,x,y,k,1);}else printf("%lld\n",query(1,1,n,x,y));}
}
上一篇:K8S---Helm
