线性代数 --- 投影与最小二乘 下(多元方程组的最小二乘解与向量在多维子空间上的投影)
创始人
2025-05-28 22:50:58
0次
在这篇文章中，我们把一元一次方程组ax=b的最小二乘问题，拓展到更为普遍的多元方程组Ax=b的最小二乘问题。之前的ax=b中的a是mx1矩阵，整个方程组只有一个未知数，a中只有一个列向量。现在我们要讨论的的方程组Ax=b有n个变量，矩阵A中有 n列。
此外，我们依然只关注方程组的个数m，大于未知数个数n的情形，也就是说观察点过多的情形。这样一来，方程组Ax=b大概率是不相容的/无解的，也就是说向量b大概率不在A的列空间C(A)内。
这里，我就不再从微积分的角度去计算最小二乘解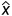
了，单单从线性代数的角度去分析方程组Ax=b。
假定Ax=b方程组为:
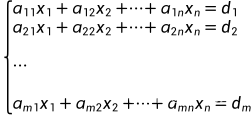
对应的矩阵A为：
其中 
方程组无解，说明b不在A的列空间上，与一元一次方程组ax=b不同的是，原来的列空间C(a)是一条直线，而这里的列空间C(A)是一个平面或者更高维度的一个子空间。要想找到方程组的近似解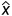，需要找到把b投影到A的列空间上，得到投影p。且，误差向量e=b-p。最后，要么基于误差向量e垂直于A中的每一个列向量col(
)，要么是利用任何垂直于A的列空间的向量都属于A的左零空间，得到误差向量e属于A的左零空间N(A)，两种方式都能求得最优解。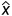
1，根据任何垂直于A的列空间C(A)的向量都属于A的左零空间N(
)，且，误差向量e也垂直于C(A)。因此，误差向量e属于A的左零空间N(A)。
关山难越，谁悲失路之人；萍水相逢，尽是他乡之客。怀帝阍而不见，奉宣室以何年？
相关内容
热门资讯
linux入门---制作进度条
了解缓冲区 我们首先来看看下面的操作： 我们首先创建了一个文件并在这个文件里面添加了...
C++ 机房预约系统（六）：学...
8、 学生模块 8.1 学生子菜单、登录和注销 实现步骤： 在Student.cpp的...
JAVA多线程知识整理
Java多线程基础 线程的创建和启动 继承Thread类来创建并启动 自定义Thread类的子类&#...
【洛谷 P1090】[NOIP...
[NOIP2004 提高组] 合并果子 / [USACO06NOV] Fence Repair G ...
国民技术LPUART介绍
低功耗通用异步接收器（LPUART） 简介 低功耗通用异步收发器...
城乡供水一体化平台-助力乡村振...
城乡供水一体化管理系统建设方案 城乡供水一体化管理系统是运用云计算、大数据等信息化手段...
程序的循环结构和random库...
第三个参数就是步长 引入文件时记得指明字符格式，否则读入不了 ...
中国版ChatGPT在哪些方面...
目录 一、中国巨大的市场需求 二、中国企业加速创新 三、中国的人工智能发展 四、企业愿景的推进 五、...
报名开启 | 共赴一场 Flu...
2023 年 1 月 25 日，Flutter Forward 大会在肯尼亚首都内罗毕...
汇编00-MASM 和 Vis...
Qt源码解析 索引 汇编逆向--- MASM 和 Visual Studio入门 前提知识ÿ...
【简陋Web应用3】实现人脸比...
文章目录🍉 前情提要🌷 效果演示🥝 实现过程1. u...
前缀和与对数器与二分法
1. 前缀和 假设有一个数组，我们想大量频繁的去访问L到R这个区间的和，...
windows安装JDK步骤
一、 下载JDK安装包 下载地址：https://www.oracle.com/jav...
分治法实现合并排序(归并排序)...
🎊【数据结构与算法】专题正在持续更新中，各种数据结构的创建原理与运用✨...
在linux上安装配置node...
目录前言1，关于nodejs2，配置环境变量3，总结 前言...
Linux学习之端口、网络协议...
端口：设备与外界通讯交流的出口 网络协议： 网络协议是指计算机通信网...
Linux内核进程管理并发同步...
并发同步并发 是指在某一时间段内能够处理多个任务的能力，而 并行 是指同一时间能够处理...
opencv学习-HOG LO...
目录1. HOG(Histogram of Oriented Gradients,方向梯度直方图)1...
EEG微状态的功能意义
导读大脑的瞬时全局功能状态反映在其电场结构上。聚类分析方法一致地提取了四种头表面脑电场结构ÿ...
【Unity 手写PBR】Bu...
写在前面 前期积累： GAMES101作业7提高-实现微表面模型你需要了解的知识 【技...